Background knowledge¶
In this page we will go through introductory bending theory, as typically covered in an introductory statics course. We will start by a quick overview of the required knowledge, and then derive our analysis from basic principles.
Our starting point will be the fact that for a body to be at rest, the vector sum of all external forces \(\mathbf{F_i}\) and moments \(\mathbf{M_i}\) acting on it must be zero.
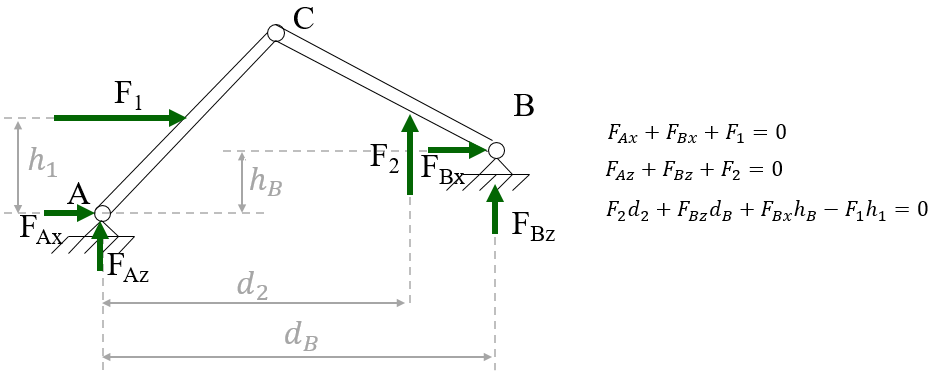
A rigid body in equilibrium (i.e. whose sum of both forces and moments equal zero)¶
Furthermore, for a system to be at rest, each of its components need to be at rest. This means that Eq. (1) must be satisfied for each component in our system.
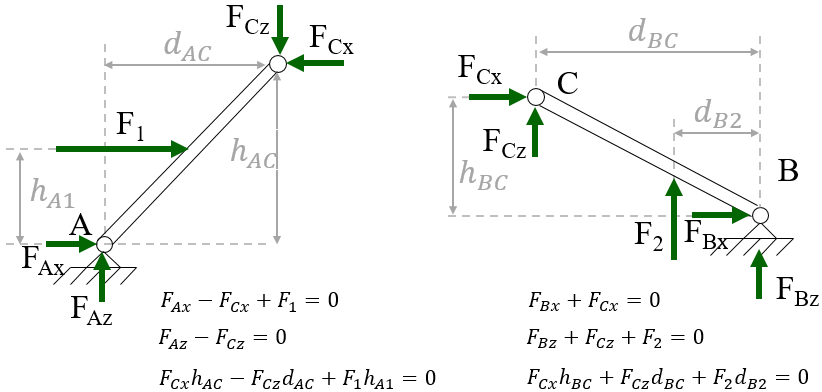
For a system to be in equilibrium, each of its subsystems must be in equilibrium.¶
Note that \(\mathbf{F_{1C}} = \mathbf{-F_{2C}}\), according to the action and reaction principle. If you are still not 100% comfortable with the action and reaction principle, you should review that before proceeding. As a self-test, the concept presented in this educational video should be completely obvious to you.
So far, we have only thought about reaction forces as applied externally to one or more rigid bodies. In other words, each rigid body has been considered to be fully contained in a single subsystem. However, Eq. (1) can tell us much more than that if we lift that restriction. This equation applies to every arbitrary subset of a body, and not only to full bodies. We are going to exploit this to a larger extent in the next section.